
Gujarat Forest Guard General Mathematics Questions and Answers: If you are the one that has applied for the Gujarat Forest Guard post, then make sure that you go through this article to take up the Gujarat Forest Guard General Mathematics Quiz. By answering the questions in Gujarat Forest Guard General Mathematics Practice Test, you will come to know your weak areas and can enhance your knowledge. Without any delay, start answering the questions in Gujarat Forest Guard General Mathematics Mock Test and submit your answers at the end to know the Gujarat Forest Guard General Mathematics Questions and Answers.
Gujarat Forest Guard General Mathematics Practice Test
1. Question : The elements of the set {x : x is an integer, x2 : 4} can be represent as …..Z….. . Here, Z refers to
A. {–2, 2}
B. {–1, 0, 1}
C. {–2, –1, 0, 1, 2}
D. {0, 1, 2}
Correct Answer: C
Sol.
2. Question : If Y = {x : x is a positive factor of the number 2p – 1(2p – 1), where 2p – 1 is a prime number}, then Y can be represent in roster form as
A. {2}
B. {1, 2}
C. {1, 2, 22, ….., 2p – 1}
D. {1, 2, 22, 23,…. 2p – 1, (2p – 1)}
Correct Answer: D
Sol.
The factors of 2p – 1(2p – 1), where 2p – 1 is a prime number, are 1, 2, 22, 23, ….., 2p – 1 and (2p – 1).
So, the roster form of given set is
{1, 2, 22, 23, ….., 2p – 1, (2p – 1)}.
3. Question : The set {x : x is a positive integer less than 6 and 3x – 1 is an even number} in roster form is
A. {1, 2, 3, 4, 5}
B. {1, 2, 3, 4, 5, 6}
C. {2, 4, 6}
D. {1, 3, 5}
Correct Answer: D
4. Question: If A B and A B, then
_
A. A is called a proper subset of B
B. A is called a super set of B
C. A is not a subset of B
D. B is a subset of A
Correct Answer: A
Sol.If A B and A B, then A is called a proper subset of B and B is called a super set of A.
5. The number of non-empty subsets of the set {1, 2, 3, 4} is
A. 15
B. 14
C. 16
D. 17
Correct Answer: A
Sol.Number of non-empty subsets = 24– 1.
6. The number of elements of the power set of a set containing m elements is
A. 2m – 1
B. m
C. m2
D. 2m
Correct Answer: D
Sol.
Let A is a set with n(A) = m
Number of elements of the power set of a given set is equal to number of subsets of the set.
n[P(A)] = 2m
7. If A = {x : x = n2, n = 1, 2, 3}, then number of proper subsets is
A. 3
B. 8
C. 7
D. None of these
Correct Answer: C
Sol.
Given that, A = {x : x = n2, n = 1,2, 3}
Number of elements in A is 3.
So, number of proper subsets = 23 – 1 = 7
8. If A = {x : x = 4n + 1, 2 £ n £ 5},then number of subsets of A is
A. 16
B. 15
C. 4
D. None of these
Correct Answer: A
9. Let A and B be two non-empty subsets of a set X such that A is not a subset of B, then
A. A is always a subset of the complement of B
B. B is always a subset of A
C. A and B are always disjoint
D. A and the complement of B are always non-disjoint
Correct Answer: D
Sol. Since, A is not a subset of B, therefore some elements of A will not be elements of B. Hence, A and complement of B are always non-disjont.
10. Which of the following is/are empty set?
A = {x : x2 + x + 1 = 0 and x Î Z} B = {x : x is a prime number and 19 < x < 23}
A. A
B. B
C. Both A and B
D. None of the above
Correct Answer: C
Sol.
The equation x2 + x + 1 = 0 is not satisfied by any integral value of x. So, A is an empty set.
Clearly, there is no prime number which lie between 19 and 23.
So, B is also an empty set
11. The set {x : x^4 = 1 and x R} is …..X…. set. Here, X refers to
A. empty
B. finite
C. infinite
D. singleton
Correct Answer: B
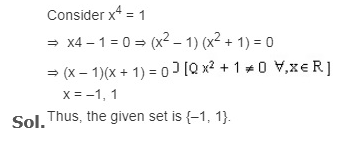
12. The universal set for the sets
A = {x : x^2 – 5x + 6 = 0} and
B = {x : x^2 – 3x + 2 = 0} having least number of elements is
A. {1, 2}
B. {1, 3}
C. {1, 2, 3}
D. {0, 1, 2, 3}
Correct Answer: C
Sol.
A = {x : x^2 – 5x + 6 = 0} = {2, 3}
B = {x : x^2 – 3x + 2 = 0} = {1, 2}
Clearly, the universal set for A and B with least elements is {1, 2, 3}.
13. Which of the following is the correct value of cot 100.cot 200.cot 600.cot 700.cot 800?
A. 1/√3
B. √3
C. -1
D. 1
Answer: (a) 1/√3
Explanation: Here, we can apply the formula –
cot A. cot B = 1 (when A + B = 900)
= (cot 20^0 . cot 70^0) x (cot 10^0 . cot 80^0) x cot 60^0
= 1 x 1 x 1/√3
= 1/√3
So, the correct value of cot 10^0.cot 20^0.cot 60^0.cot 70^0.cot 80^0 = 1/√3
14. If a sin 45^0 = b cosec 30^0, what is the value of a^4/b^4?
A. 6^3
B. 4^3
C. 2^3
D. None of the above
Answer: (b) 4^3
Explanation: Given a sin 45^0 = b cosec 30^0
So, a/b = cosec 30^0/ sin 45^0
a/b = 2/( 1/√2)
a/b = 2√2/1
a^4/b^4 = (2√2/1)^4
a^4/b^4 = 64/1
or,
a^4/b^4 = 4^3
15. If the value of α + β = 900, and α : β = 2 : 1, then what is the ratio of cos α to cos β ?
A. 1 : 3
B. √3 : 1
C. 1 : √3
D. None of the above
Answer: (c) 1 : √3
Explanation: Given α + β = 90^0, and α : β = 2 : 1
So, we can say that 2x + x = 90^0
3x = 90^0, which give
x = 30^0
So, α = 2x = 60
β = x = 30
cos α / cos β = cos 60^0 / cos 30^0
=> (1/2) / (√3/2)
or, 1/2 * 2/√3
= 1/√3
Or the ratio between cos α : cos β = 1 : √3
16. Which of the following statements is not correct?
A. log10 10 = 1
B. log (2 + 3) = log (2 x 3)
C. log10 1 = 0
D. log (1 + 2 + 3) = log 1 + log 2 + log 3
Answer: Option B
Solution:
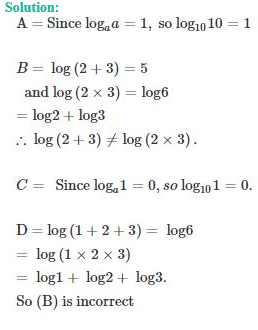
17. If log 2 = 0.3010 and log 3 = 0.4771, the value of log5 512 is:
A. 2.870
B. 2.967
C. 3.876
D. 3.912
Answer: Option C
Solution:

18. If log 27 = 1.431, then the value of log 9 is:
A. 0.934
B. 0.945
C. 0.954
D. 0.958
Answer: Option C
Solution:
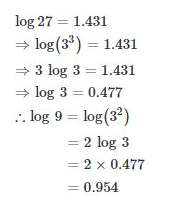
19. The value of 1 + i2 + i4 + i6 + … + i2n is
(a) positive
(b) negative
(c) 0
(d) cannot be evaluated
Correct option: (d) cannot be evaluated
Solution:
1 + i2 + i4 + i6 + … + i2n = 1 – 1 + 1 – 1 + … (–1)n
20. If a + ib = c + id, then
(a) a^2 + c^2 = 0
(b) b^2 + c^2 = 0
(c) b^2 + d^2 = 0
(d) a^2 + b^2 = c^2 + d^2
Correct option: (d) a2 + b2 = c2 + d2
Solution:
Given,
a + ib = c + id
⇒ |a + ib| = |c + id|
⇒ √(a^2 + b62) = √(c^2 + d^2)
Squaring on both sides, we get;
a^2 + b^2 = c^2 + d^2
★★ You Can Also Check ★★



