
SSC CPO Quantitative Aptitude Questions & Answers: Mastering the SSC CPO Quantitative Aptitude section requires dedicated practice. To aid your preparation for the SSC CPO Exam, we present an article with SSC CPO Quantitative Aptitude Questions in both Hindi and English. Take the quiz below to gauge your proficiency and identify areas that need further practice, as well as your strong areas.
★★ SSC CPO Free Mock Tests ★★
Within this article, we have compiled the Important Quantitative Aptitude Questions for SSC CPO. As candidates have plenty of time, they should take this preparation period seriously and utilize the SSC CPO Quantitative Aptitude Questions quiz for practice. Lastly, remember to check your score to evaluate your performance in the quiz provided below.
SSC CPO Quantitative Aptitude Questions withe Answers
1. A train x running at 74 km/h crosses another train y running at 52 km/h in the opposite direction in 12 seconds. If the length of y is two-thirds that of x, then what is the length of x (in m)?
a) 168
b) 252
c) 210
d) 200
e) None
Answer: b
Explanation:
Relative speed = 74 + 52 = 126 km/h = 126 × 5 / 18 = 35 m/s
Relative distance travelled = 12 × 35 = 420 m
Let the length of train x be “a” m.
Then, length of train y = 2 / 3a am
Total length of both trains = 420 m
=>a + 2 / 3a = 420 m
=> 5 / 3 a = 420
=> a= 420 × 3 / 5 = 252 m
Therefore, the length of train x is a = 252 m.
2. A is twice as good a workman as B and together they finish a piece of work in 13 days. In how many days will B alone finish the work?
a) 18.5
b) 21
C) 39
d) 42
e) None
Answer: c
Explanation:
Let the efficiency of B be x.
Then, the efficiency of A = 2x.
Therefore, total work = (x + 2x) × 13 = 39x.
Now, time taken by B alone to finish the work = 39 x / x = 39 days
(Directions 3-5). The given bar graph shows the number of students of two schools over a period of six years.
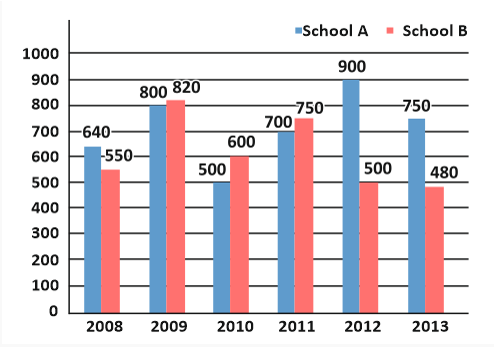
3. In the bar graph, in which year is the sum of the students from schools A and B taken together, the minimum?
a) 2012
b) 2010
C) 2013
d) 2011
e) None
Answer: b
Explanation:
Sum of the students from schools A and B taken together in 2008
= 640 + 550 = 1190
Sum of the students from schools A and B taken together in 2009
= 800 + 820 = 1620
Sum of the students from schools A and B taken together in 2010
= 500 + 600 = 1100
Sum of the students from schools A and B taken together in 2011
= 700 + 750 = 1450
Sum of the students from schools A and B taken together in 2012
= 900 + 500 = 1400
Sum of the students from schools A and B taken together in 2013
= 750 + 480 = 1230
Hence, in 2010, the sum of the students from schools A and B taken together is the minimum.
4. In the bar graph, what is the ratio of the students taken for the years 2009, 2011, 2013 together from school A to the students taken for the years 2008, 2012, 2013 together from school B?
a) 17 : 25
b) 25 : 17
c) 18 : 25
d) 25 : 18
e) None
Answer: b
Explanation:
Total students taken for the years 2009, 2011, 2013 together from school A = 800 + 700 + 750 = 2250
Total students taken for the years 2008, 2012, 2013 together from school B = 550 + 500 + 480 = 1530
Hence, Required ratio = 2250 : 1530 = 25 : 17
5. In the bar graph, what is the ratio of the average of the total students from school A to the average of the total students from school B?
a) 370 : 429
b) 429 : 799
c) 799 : 429
d) 429 : 370
e) None
Answer: d
Explanation:

6. A circle is inscribed in a triangle ABC . It touches sides AB, BC and AC at points R, P and Q, respectively. If AQ = 3.5 cm, PC = 4.5 cm and BR = 7 cm, then the perimeter (in cm) of the triangle ABC is:
a) 45
b) 28
c) 15
d) 30
e) None
Answer: d
Explanation:
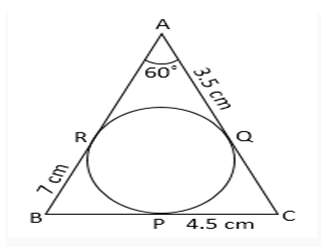
Given:
AQ = AR = 3.5 cm (tangents drawn from the same point on the circle)
Similarly, PC = QC = 4.5 cm
And BR = BP = 7 cm
Now, perimeter of ∆ABC = AB + BC + CA
= AR + RB + BP + PC + CQ + QA
= 3.5 + 7 + 7 + 4.5 + 4.5 + 3.5 = 30 cm
7. One side of a rhombus is 13 cm and one of its diagonals is 10 cm. What is the area of the rhombus (in cm2)?
a) 30
b) 60
c) 120
d) 90
e) None
Answer: c
Explanation:
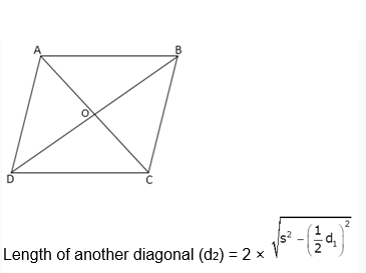
We know that the diagonals of a rhombus bisect each other at right angles.
So, CO = 10/2 = 5 cm
Since, CD = 13 cm
Here, triangle COD is a right-angle triangle.
OD2 = CD2 – CO2
OD2 = 132 – 52 = 169 – 25 = 144
OD = 12 cm
Thus, BD = 2 × OD = 2 × 12 = 24 cm
Hence, Area of the rhombus = 1 / 2 d1 d2 = 1 / 2 × 10 ×24 = 120
8. If 4(cosec257° – tan233°) – cos90° – ytan266° tan224° = y/2 the value of y is:
a) 3/8
b) 8
c) 1/3
d) 8/3
e) None
Answer: d
Explanation:
Given, 4(cosec257° – tan233°) – cos90° – ytan266° tan224° = y/2
⇒4(sec233° – tan233°) – 0 – ycot224° tan224° = y/2
⇒4 – y = y/2 (Since, sec2θ – tan2θ = 1)
⇒3 / 2 y = 4
⇒y = 8 / 3 .
9. Three successive discounts 22%, 17% and 11% are equivalent to a single discount of:
a) approximately 45%
b) approximately 5%
c) approximately 42%
d) approximately 25%
e) None
Answer: c
Explanation:
Let the Marked Price of the product be 100x.
Then, price after first discount of 22% = 100x – (100x) × 22% = 100x – 22x = 78x
Price after second discount of 17% = 78x – (78x) × 17% = 78x – 13.26x = 64.74x
And price after third and final discount of 11% = 64.74x – (64.74x) × 11% = 64.74x – 7.12x = 57.62x
Total discount in price = 100x – 57.62x = 42.38x ≈ 42x
i.e. approximately 42%
Method 2:-
Let the marked price = ₹100
Then, the selling price
= 100×78%×83%×89%
≈ ₹57.6
Discount = 100 − 57.6 = ₹42.4
Discount% = (42.4/100)×100% = 42.4%
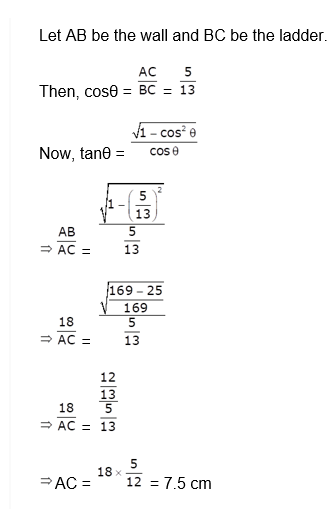
10. A ladder leaning against a wall makes an angle θ with the horizontal ground such that cosθ = 5/13. If the height of the top of the ladder from the wall is 18 m, then what is the distance (in m) of the foot of the ladder from the wall?
a) 19.5
b) 13
c) 7.5
d) 18
e) None
Answer: c
Explanation:
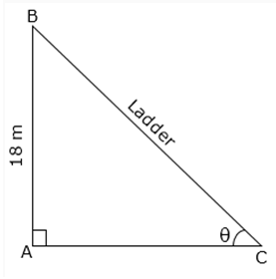
 11. The given histogram shows the height of the students
11. The given histogram shows the height of the students
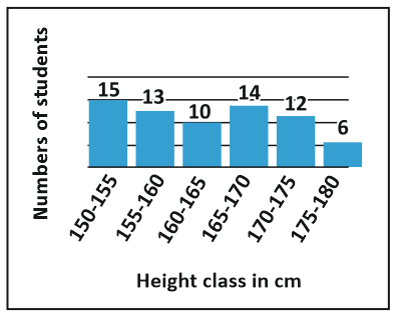
The difference between the number of students whose height is between 150-155 cm and the number of students whose height lies between 175 – 180 cm is:
a) 3
b)
c) 9
d) 7
e) None
Answer: c
Explanation:
Number of students whose height is between 150-155 cm = 15
Number of students whose height is between 175-180 cm = 6
Required, difference between the number of students whose height is between 150-155 cm and the number of students whose height lies between 175-180 cm = 15 – 6 = 9
12. What is the least number which when divided by 15, 18 and 36 leaves the same remainder 9 in each case and is divisible by 11?
a) 1269
b) 1089
c) 1080
d) 1071
e) None
Answer: b
Explanation:
In order to find such a number, we have to first calculate LCM of 15, 18 and 36 which is 180.
Now, that number will be in format of 180k + 9, where k is any positive integer.
Now, this number must be divisible by 11.
By going through options, we can find out that such a number is 1089, which satisfies both the conditions i.e. k = 6. Hence, option b is the answer.
13. Two numbers are in the ratio 7 : 11. If their HCF is 28, then the difference between the two numbers is:
a) 28
b) 196
c) 112
d) 308
e) None
Answer: c
Explanation:
Since the absolute ratio of the numbers and HCF of the numbers are given, the two numbers are 28 × 7 = 196 and 28 × 11 = 308.
Now, their difference = 308 – 196 = 112
14. PA and PB are two tangents from a point P outside the circle with centre O. If A and B are points on the circle such that ∠APB = 128°, then ∠OAB is equal to:
a) 64°
b) 72°
c) 52°
d) 38°
e) None
Answer: c
Explanation:
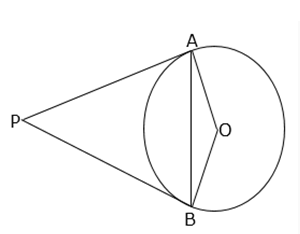
Given:
∠APB = 128°
Now, ∠AOB = 180° – ∠APB = 180° – 128° = 52°
In ∆OAB,
OA = OB = radius
15. If 14331433 × 1422 × 1425 is divided by 12, then what is the remainder?
a) 3
b) 9
c) 6
d) 8
e) None
Answer: c
Explanation:
Remainder, when 14331433 × 1422 × 1425 is divided by 12.
Divide individual number by 12, obtain remainder and then multiply them.
1 × 6 × 9 = 54
Now, divide 54 by 12 and obtain remainder, that is 6.
Hence, the remainder, when 14331433 × 1422 × 1425 is divided by 12, is 6.
16. The average weight of A, B and C is 65 kg. If the average weight of A and B is 63.5 kg, and the average weight of A and C is 67.5 kg, then the weight of A (in kg) is:
a) 65
b) 67
e) 60
d) 68
e) None
Answer: b
Explanation:
Total weight of A, B and C = 3 × 65 = 195 kg.
Total weight of A and B = 2 × 63.5 = 127 kg.
Weight of C = Total weight of A, B and C – Total weight of A and B = 195 – 127 = 68 kg.
Total weight of A and C = 2 × 67.5 = 135
Hence, Weight of A = Total weight of A and C – Weight of C = 135 – 68 = 67 kg.
17. In ∆ABC, BD ⊥ AC at D . E is a point on BC such that ∠BEA = x°. If ∠EAC = 46° and ∠EBD = 60°, then the value of x is:
a) 76°
b) 68°
c) 78°
d) 72°
e) None
Answer: a
Explanation:
In ∆OAD,
∠OAD = ∠EAC = 46° (given),
And ∠ADO = 90° (BD ⊥ AC)
Therefore, ∠AOD = 180° –∠OAD – ∠ADO = 180° – 46° – 90° = 44°
(Sum of all three angles of a triangle is 180°)
Now, in ∆BOE,
∠OBE = ∠EBD = 60° (given),
And ∠BOE = ∠AOD = 44° (Opposite angles)
Now, ∠BEO = x = 180° – ∠OBE – ∠BOE = 180° – 60° – 44° = 76°
(Sum of all three angles of a triangle is 180°)
18. If a nine-digit number 785x3678y is divisible by 72, then the value of (x – y) is:
a) 0
b) -2
c) -1
d) 2
e) None
Answer: d
Explanation:
We know that 72 = 9 × 8
Therefore, the given number must be divisible by 9 and 8.
First, divisibility rule of 8: Last three digits of the number must be divisible by 8.
Therefore, the last three digits are 78y.
In addition, y = 4. (since we have to calculate least value)
Now, divisibility rule of 9: Digital sum of the number must be divisible by 9.
Now, digital sum of 785×36784 = 7 + 8 + 5 + x + 3 + 6 + 7 + 8 + 4
= 48 + x
The next multiple of 9 after 48 is 54.
Therefore, x = 54 – 48 = 6
Now, required x – y
= 6 – 4 = 2
19. The given pie chart represents the popularity of ice-cream flavours in the year 2005 and 2015.
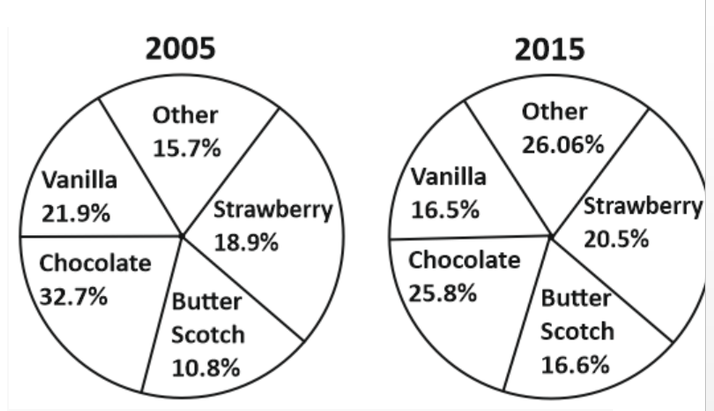
If a percentage point shift results in annual additional sales Rs.10,000, how much (in Rs.), did the combined annual strawberry and butterscotch sales increase from 2005 to 2015?
a) Rs.65,000
b) Rs.74,000
c) Rs.37,000
d) Rs.10,000
e) None
Answer: b
Explanation:
Combined annual sales of strawberry and butterscotch in 2005 (in %)
= 18.9 + 10.8 = 29.7%
Combined annual sales of strawberry and butterscotch in 2015 (in %)
= 20.5 + 16.6 = 37.1%
Increase in combined annual strawberry and butterscotch sales from 2005 to 2015 (in % points) = 37.1 – 29.7 = 7.4%
Increase in combined annual strawberry and butterscotch sales from 2005 to 2015 (in ₹) = 7.4 × 10000 = 74000
20. A takes 2 hours 30 minutes more than B to walk 40 km. If A doubles his speed, then he can make it in 1 hour less than B . How much time (in hours) does A require for walking a 40 km distance?
a) 7
b) 5
c) 6
d) 9
e) None
Answer: a
Explanation:
Let the time taken by B be “x” hours.
Then, time taken by A at his usual speed = (x + 2.5) hours
And time taken by A at double of his usual speed = (x – 1) hours
Now, as speed is doubled for A, therefore, time will be half,
2(x – 1) = (x + 2.5)
⇒2x – 2 = x + 2.5
⇒x = 2.5 + 2 = 4.5 hours
Therefore, Time taken by A at his usual speed = x + 2.5
= 4.5 + 2.5 = 7 hours



